Moving Average
The Basics
Moving averages are used to smooth out market volatility and identify changes in trend.
Indicator Type
Trend follower
Markets
All cash and futures, not options
Works Best
Trending markets
Formula
Moving averages can be calculated from open, high, low, close or some combination of these data. Simple averages are means of the data. Other averages assign higher significance to recent data than to older data.
Technician allows you to calculate the average based on open, high, low, close or adjusted close data.
You also have a choice of several average types as follows.
- Simple: mean (average) of the data.
- Exponential: newer data are weighted more heavily geometrically.
- Time Series: Calculates a linear regression trendline using the “least squares fit” method.
- Triangular: Weighted average where the middle data are given the most weight, decreasing linearly to the end points.
- Variable: An exponential moving average with a volatility index factored into the smoothing formula. The Variable Moving average uses the Chande Momentum Oscillator as the volatility index.
- VIDYA: An exponential moving average with a volatility index factored into the smoothing formula. The VIDYA moving average uses the Standard Deviation as the volatility index. (Volatility Index Dynamic Average)
- Weighted: newer data are weighted more heavily arithmetically.
- Welles Wilder: The standard exponential moving average formula converts the time to a fraction using the formula EMA% = 2/(n + 1) where n is the number of days. For example, the EMA% for 14 days is 2/(14 days +1) = 13.3%. Wilder, however, uses an EMA% of 1/14 (1/n) which equals 7.1%. This equates to a 27-day exponential moving average using the standard formula.
Parameters
Commodities traders use 50-day simple averages. Bond traders use 10-day weighted averages. Intraday traders use 3- and 5-day averages of highs and of lows. Stock traders use 200- and 50-day averages. Long-term traders use 40 and 52-week averages. Day traders use hourly and minute.
Theory
The direction of the moving average (higher, lower or flat) indicates the trend of the market and its slope indicates the strength of the trend. Longer averages are used to identify longer-term trends and shorter averages are used to identify shorter-term trends. Many trading systems utilize moving averages as independent variables and market analysts frequently use moving averages to confirm technical breakouts.
Interpretation
Typical analysis involves price crossovers with the average. It is a lagging indicator but can confirm that a change in trend has taken place. When coupled with a trend line or support/resistance violation, the signal becomes quite reliable. Averages give traders an idea of support and resistance areas, but they should not be used alone to determine trade triggers. Overshoots of averages are common although using an envelope of the averages of highs and of lows can help mitigate this.
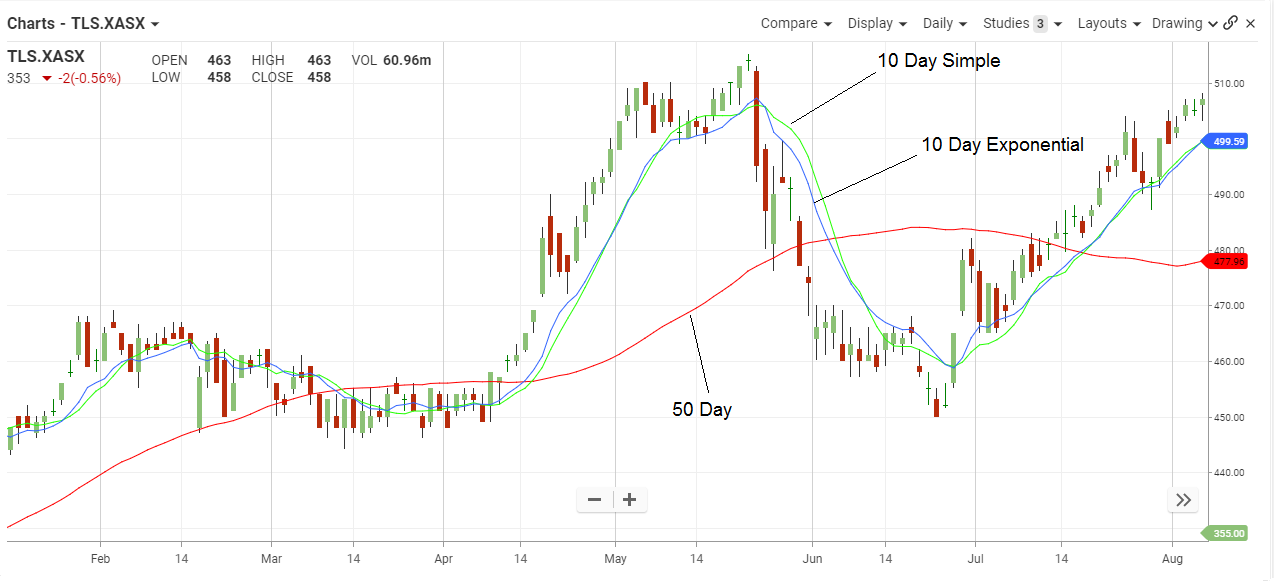
Telstra offers short-term analysis via the 10-day simple and exponential average. The latter reacts to market changes faster than the former and crossovers between the two can help confirm short-term trend changes.
The 50-day average gives traders an idea of the intermediate-term trend and extreme movements of price away from the average can indicate overbought or oversold conditions Price crossovers indicate changes in the intermediate-term trend.
Math
Moving Averages
| Simple = | P + P1 + … + P(n-1) |
| n | |
| Weighted = | n*P + (n-1)*P1 + (n-2)*P2 + … + P(n-1) |
| 1 + 2 + 3 + … + n | |
| Exponential = | P + aP1 + a2P2 + … + a(n-1) P(n-1) |
| 1 + a + a2 + … + a(n-1) | |
| Welles Wilder = | P + wP1 + w2P2 + … + w(n-1) P(n-1) |
| 1 + w + w2 + … + w(n-1) | |
| Variable = | P + (a*b)P1 + (a*b)2P2 + … + (a*b)(n-1) P(n-1) |
| 1 + (a*b) + (a*b)2 + … + (a*b)(n-1) | |
| Vidya = | P + (a*bv)P1 + (a*bv)2P2 + … + (a*bv)(n-1) P(n-1) |
| 1 + (a*bv) + (a*bv)2 + … + (a*bv)(n-1) | |
| Triangular = | Same as weighted average except the middle data gets the highest weight and the ends get arithmetically lower weights |
| Where: P = | current price |
| P1 = | price 1 period ago |
| P2 = | price 2 periods ago |
| a = | smoothing constant 2/(n+1) |
| w = | smoothing constant 1/n |
| v = | a*b and is variable |
| b = | absolute value (F(P)/100) |
| F = | Chande Momentum Oscillator (CMO) with Period 9 |
| n = | user-defined number of periods for the average |
| bv = | 5 period std dev / 20 period std dev |
